

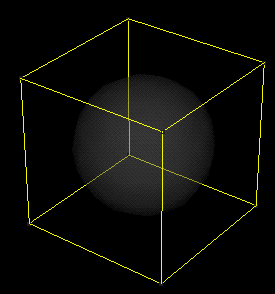
The above sphere is an example of a subdivision surface. The surface is drawn X-ray smooth shaded to show the CVs around the object. A few things are immediately noticable:
| NURBS | Polys | Subdivs | |
| Geometrically Smooth | Y | Y | |
| Arbitrary topology | Y | Y | |
| Hierarchy | Y |
Subdivision surfaces combine the best properties of NURBS and polygons. However it is better to think of them as being enhanced NURBS rather than being enhanced polygons. Manipulating the CVs on a subdivision surface deforms the surface in a way that will be familiar to anyone who has modelled with NURBS surfaces. Subdivision surfaces provide most of the advantages of NURBS surfaces, with the addition of two important properties:
The subdivision surface can be thought of as being a little like
the result of a polygon smooth operation. When polygons are smoothed,
the corners of the polygon model are progressively chopped off,
leading to a smoother and smoother surface. However this is an
infinite process, since it is always possible to smooth more. In a
similar way, a subdivision surface is the end result of an infinite
number of smoothing operations on an initial mesh object. The end
result of an infinite number of subdivisions is called a limit
surface A difference from the poly smooth operation is that
the limit surface of a subdivision model is almost everywhere a
uniform cubic B-spline surface. This is very important because it
means that the subdivision surface is actually geometrically smooth in
the same way that a B-spline surface is smooth, in contrast to a
smoothed poly mesh which is always a faceted approximation to a
smooth surface. As a result, subdivision surfaces provide the user
with a tool that retains the smoothness properties of NURBS geometry
while providing the extra advantages of arbitrary toplogy and
multi-resolution editing.
Subdivision surfaces allow the arbitrary topology of polygons while
retaining the smooth surface properties of NURBS. Note that the
subdivision surface does not have to be closed - it can have any
topology that a polygon mesh can have.
Once these extra isoparms have been inserted into a NURBS surface
(as at above right) it becomes difficult to make large scale smooth
changes, since now a large number of CVs needs to be moved
consistently in order to generate the required effect. As a results,
deformation tools such as lattices are often used to provide simpler
large scale control over a complex NURBS surface.
Subdivision surfaces in contrast allow the user to add small
features onto large surfaces because they are hierarchical surfaces,
that is they can be edited at a number of different levels of
resolution without requiring insertion of extra detail all over the
surface. Large scale changes and fine scale changes can be made by
working with different sets of CVs that exist simultaneously on the
surface.
These multiple distinct sets of CVs are a feature of subdivision
surfaces, and take some getting used to. The CVs that are visible at
first are called the base mesh, also called the coarsest
level or level 0. There are actually an infinite number
of levels of CVs available at finer levels. Here is an example of the
same surface with CVs at the base mesh (top left) and the next three
finer levels shown:
Clearly there are more CVs at finer levels, and therefore any given
CV at a finer level will influence a smaller region of the surface.
Thus when modelling an object made from a subdivision surface, the
user can tweak CVs on the base mesh to make large scale changes to the
model, and then move to finer levels to provide more detailed control
over a smaller region. The user can move freely between the different
levels applying tweaks to CVs. All previously applied tweaks will be
preserved as the model is being edited.
The multiple levels of CVs can be a bit hard to understand. The
base mesh is all that is needed to define a subdivision surface
completely. This mesh contains all the CVs at the base level, and from
these CVs the surface can be computed. Also from these CVs, the CVs at
all finer levels can be computed, since there are well defined rules
for the positions of CVs at a level given the positions of CVs at the
coarser level. If a CV at a base level is moved, all CVs at finer
levels close to this CV will also be moved. To ensure tweaks to CVs at
finer levels are not lost when the user moves a CV at a coarser level,
the tweaks on each CV are stored internally as offsets from their
original position. This means that when a base CV is moved that causes
a CV that has already been tweaked to move, the tweak will be
reapplied after the move, so that all editing information is
preserved.
Imagine building a NURBS surface in Maya. Then rebuild that
surface to a higher resolution with Keep Originals on. The end
result is a pair of surfaces that look the same, but having different
numbers of CVs. Imagine tweaking a CV on the original surface. There
would be a large scale deformation on the original surface. In
addition, the rebuilt surfaces would deform to produce exactly the
same surface, since it is connected via history to the original
surface. Now move a CV on the rebuilt surface. This would produce a
more localised deformation on the surface than the result of moving
the CV on the original surface. Now go back to the original surface
and moving another CV. This would again produce a large scale
deformation, which would be propagated to the rebuilt
surfaces. However because tweaks to the rebuilt surface are stored in
with that rebuilt surface, these tweaks would not be lost but would be
added to the changes made to the surface as a result of the history
propagation. Here is the above in pictures for a NURBS plane:
Using the above process, the user can model a surface at different
levels of resolution and be sure that all the tweaks applied at the
different levels are preserved. Subdivision surfaces provide the same
workflow, but it comes 'for free' since this hierarchical structure is
built into the surface definition itself. There is only one surface
(equivalent to the rightmost surface in the above example) but the CVs
exist at a number of levels.
Another feature of the above NURBS example is that once the
original surface is defined and the rebuild rules are specified, the
positions of the CVs on all of the rebuilt surfaces are exactly
defined as well. The user may tweak them, but the original positions
are determined only by the original surface from which they are
rebuilt. In the same way, the CVs on a finer level of a subdivision
surface are defined exactly by the positions of the CVs at coarser
levels, although they can still be tweaked.
Note that CVs exist all over the surface at all levels of
detail. At first sight this might appear to lose the advantage of
adding detail only where needed, as in the example picture at the top
of this section. However since the positions of CVs at any level can
be computed from the CVs at a coarser level plus any tweaks that were
applied directly to that CV, we only need to store CVs that have been
tweaked by the user from their original position. All other CV
positions are defined by the base mesh, and can be computed only when
they are needed.
Extraordinary points These are points on the surface where
the CV has more or less than 4 neighbouring CVs.
Base mesh The coarsest level of CVs that define a
subdivision surface. Also known as the level 0 mesh.
Level CVs exist at an infinite number of levels,
corresponding to different levels of resolution. The base mesh is the
coarsest level. It is a good idea to refer to levels as "coarser" and
"finer" rather than "higher" or "lower" since people have different
ideas about which direction "higher" implies.
Limit surface The actual subdivision surface itself, which the
result of an infinite number of subdivision operations.
Arbitrary toplogy
Compared with NURBS
NURBS are a powerful modelling tool that are suitable for many types
of model generation. They generate smooth surfaces that are easy to
work with. However NURBS surfaces are parametrically rectangular. That
is they can be thought of as flexible and stretchable sheets, which
can be pulled into any shape but still retain their rectangular
toplogy. This means certain types of model cannot be generated with a
single NURBS surface eg hands. Such objects must therefore be
modelled with multiple NURBS surfaces, and this introduces complexity
since these surfaces then have to join smoothly at their common
boundaries, and retain that smoothness under deformation.
Compared with Polygons
In contrast to NURBS, polygons are able to model arbitrary topology
objects without difficulty. However the underlying surface is always
faceted.
Hierarchical structure
As well as the rectangular topology restriction, NURBS have another
disadvantage, in that it is difficult to add small features to large
surfaces. To add a small feature onto a NURBS surface, extra isoparms
must be inserted at that point. However these isoparms cross the whole
surface, introducing rows of patches all the way across the surface,
even in areas where it is not needed. This is commonly a problem when
heads are modelled as single NURBS surfaces. To provide more detail
around the nose, for example, extra isoparms are inserted which then
wrap all the way around to the back of the neck. An extreme example is
below, where the user wishes to add detail at a number of points
diagonally across the surface. The end result is the surface at top
right, although an ideal situation would only insert the detail where
needed, as in the bottom figure:




An analogy

For each of these three pairs of surfaces the left surface is base
surface, and the right surface has been rebuilt from the left surface
with a greater density of isoparms:
Modelling with Subdivision surfaces compared with NURBS and polygons
In general a model created with subdivision surfaces will have far
fewer surfaces that one created with NURBS. Because of the arbitrary
topology and hierarchical properties of the subdivision surface, it is
often not necessary to use multiple surfaces to create a model. This
makes modelling work much easier, since there is less need to worry
about operations such as trimming, stitching, aligning etc. Also
deformer tools such as lattices will be less necessary. In some ways
the base mesh is a more intuitive deformer than a lattice because the
base mesh follows the shape of the surface, which is not necessarily
true of a lattice.
Glossary
Martin Watt